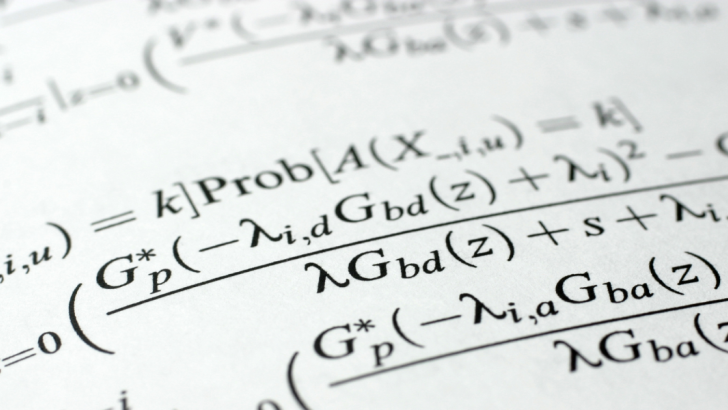Alessio Figalli, classe 1984, è il secondo italiano a vincere la prestigiosissima Medaglia Fields, assegnata ogni quattro anni dall’Unione Matematica Internazionale a giovani studiosi di meno di quarant’anni come riconoscimento per gli straordinari contributi ottenuti in campo matematico e come incentivo per i prossimi. Prima di lui, in Italia, a vincerla fu solo Enrico Bombieri, nel 1974.

Il risultato non stupisce, nonostante si tratti di quello che viene considerato il più alto riconoscimento nel settore, una sorta di Premio Nobel, vista la carriera fulminante di Figalli.

La matematica si dice sia uno di quei settori in cui, diversamente da altri (la letteratura, ad esempio: Henri-Pierre Roché scrisse Jules e Jim quando aveva una settantina d’anni), i risultati, se arrivano, arrivano presto.

E il caso di Figalli non fa eccezione. Diplomatosi al classico, con l’idea, forse, di diventare ingegnere, entra invece alla Normale di Pisa e si laurea a 22 anni sotto la guida di Luigi Ambrosio, a sua volta allievo di un grande matematico italiano: Ennio De Giorgi. Ed è nel filone di questa prestigiosa scuola di ricerca che Alessio Figalli si inserisce, dice infatti: “Il mio dominio è l’analisi. Un problema su cui ho lavorato molto è il trasporto ottimale. Ci sono tante casistiche in cui questo tema riappare. In problemi di natura geometrica ad esempio, ma anche in meteorologia. Per esempio hanno scoperto che se una nuvola deve spostarsi, le particelle che la compongono seguiranno nel tempo un trasporto ottimale”.

Di cosa si tratta il trasporto ottimale (insieme ad altre curiosità sulla matematica e i matematici) lo abbiamo chiesto a Paolo Ciatti, docente di analisi matematica all’Università di Padova.

Ma cosa sono più in generale l’analisi funzionale e il calcolo delle variazioni, i temi portanti della ricerca di Figalli e prima ancora di Ambrosio e De Giorgi?

Si consideri che una funzione è una relazione che ad un elemento di un insieme ne associa un altro di un secondo insieme (e si dice infatti che il secondo è funzione del primo): ecco, l’analisi funzionale moderna, del XX secolo, come scrive lo stesso De Giorgi: “considera una famiglia infinita di funzioni e ha l’interesse ad organizzarle in qualche modo in maniera da poter studiare le proprietà di questa famiglia organizzata che si chiama spazio funzionale”.

Il calcolo delle variazioni invece rappresenta tipicamente problemi di “ricerca di massimo e minimo”. Caso celebre è il problema di Didone, la pragmatica regina di Tiro che esiliata dal fratello raggiunse la terra dei Getuli e lì ottenne dal re di poter avere un pezzo di terra. Quanta? Quanta sarebbe riuscita a ricoprirne con una pelle di bue. Lei allora fece la pelle a striscioline e le legò per produrre una corda con cui circondare l’area ma si chiese: che forma deve avere la corda perché racchiuda la maggior superficie possibile? Questo è un tipico esempio di problema variazionale. A tal proposito Figalli spiega: “il problema di Didone può essere visto in due modi diversi. Cioè fisso la lunghezza della corda e mi chiedo qual è l’area massima che posso racchiudere dentro la figura che faccio descrivere oppure fisso l’area che voglio racchiudere e cerco la lunghezza minima della corda che la racchiude. Si tratta quindi proprio di un problema di ricerca del minimo”.

È interessante osservare come il calcolo delle variazioni appaia sia nel quesito diciannove del Programma formulato da Hilbert ad inizio Novecento per formalizzare la matematica e dimostrarne la “potenza” e che venne risolto da De Giorgi e John Nash (Premio Nobel per l’economia noto per la teoria dei giochi) indipendentemente, così come appare anche nel quesito ventitré. Ha a che vedere insomma con questioni fondazionali della disciplina, cioè riguarda le verità da assumere come capisaldi o che dagli assiomi di base possono essere dimostrate. De Giorgi fu infatti uno dei primi ad avere il coraggio di riprendere l’attività di Kurt Gödel lì dove il logico e matematico l’aveva portata all’inizio degli anni Trenta e di affacciarsi sull’orlo dell’abisso cui il pensatore si era sporto. Abisso su cui altri prima di lui, in ambiti affini, si erano trovati a provare le vertigini, se si pensa all’impatto che ebbero le geometrie non euclidee sul pensiero matematico: rette parallele che si incontrano all’infinito? Che significa?

Tutto questo è molto affascinante, osservando poi che, appunto, i grandi (e giovani) matematici di oggi altro non fanno che proseguire lungo un sentiero già tracciato e a volte interrotto, o all’apparenza cieco, magari trovando nuove aperture.

E nonostante Alessio Figalli si inserisca a pieno titolo, come visto, nella tradizione matematica italiana, è quasi più conosciuto all’estero che in Italia: ha infatti preso il dottorato in in cotutela tra Pisa e Lione, sotto la supervisione di Luigi Ambrosio e Cédric Villani, nell’ottobre del 2007 ha vinto un posto da ricercatore al CNRS (Centre National de la Recherche Scientifique), l’equivalente del CNR italiano, e nel 2008 si è trasferito all’Ecole Polytechnique di Parigi col titolo di “Professeur Hadamard” per poi, nel 2009, diventare professore associato, e nel 2011 ordinario, all’Università del Texas ad Austin. Nel 2016 ha infine deciso di rientrare in Europa e ha preso una cattedra al Politecnico di Zurigo.

Carriere del genere, rimanendo nel nostro Paese, sarebbero forse impensabili. Ne abbiamo parlato con Davide Vittone, anch’egli allievo di Ambrosio e ricercatore all’università di Padova, che conosce Figalli personalmente da diversi anni.

Ma com’è possibile raggiungere vette di questo tipo? Serve una mente “plusdotata”? Per Ciatti la risposta è duplice: sì, esistono i geni matematici, ma c'è anche chi invece si applica molto e con dedizione può portare il suo contributo alla causa, e Vittone specifica: un grande risultato si ottiene appassionandosi ai propri problemi, restandoci sopra con la testa anche per anni, riempiendo pagine di calcoli, studiando, ma poi serve quel guizzo che porta a qualcosa di nuovo.