Esistono molti modi per guardare a un romanzo. Uno è con gli occhi del critico letterario, che ne valuta il valore artistico. Un altro è con gli occhi del semplice lettore, che osserva come il testo sia piacevole e godibile. Un altro ancora, tra i tanti, è con gli occhi di chi cerca i luoghi dove le discipline si incontrano ed esaltano l’unità profonda della cultura umana.

Chi scrive non è un critico letterario, ma è un semplice lettore con un certo interesse per il rapporto tra arte e scienza. Dunque nel leggere Gli occhi di Eulero scritto da Paolo Maria Mariano (Mimesis, 2020, pagg. 172, euro16,00) ha utilizzato occhi letterariamente ingenui, potenziati in qualche modo dagli occhiali dell’interdisciplinarità. Alla luce di questi occhi il libro appare godibile e interessante, anche perché (proprio perché) costringe a recuperare molte nozioni di storia della scienza, di storia della filosofia, di storia della letteratura, di storia tout court. Ed ha un grande merito: dimostrare che anche i grandi della scienza non vivono in un mondo separato, in una sorta di paradiso della ragione, ma vivono in un tempo storico, denso di fatti e di persone, di sentimenti e contraddizioni. Insomma, vivono la vita. È questo, se abbiamo ben capito, quanto vuole l’autore, che è un fisico – insegna Meccanica teoria all’Università di Firenze e coordina il Gruppo di Meccanica Teorica al Centro di Ricerca Matematica Ennio De Giorgi di Pisa – che si interessa di filosofia della scienza.

Voce narrante del romanzo è un signore che, da ragazzo, era stato garzone nella casa di Eulero, a San Pietroburgo. Eulero è un grande matematico, uno dei più grandi di ogni tempo. E il ragazzo viene assunto col compito di spalare il carbone, spaccare la terra, aiutare in cucina e, quando era il momento, portare i testi del suo padrone – ah, quanto scriveva, Eulero – in tipografia.

Ma il ragazzo non ha voglia di restare un garzone, ha voglia di imparare. In casa di Eulero impara a leggere e a scrivere e impara, poi, la matematica e, come si dice, fa carriera: con gli anni e con la calda raccomandazione di Eulero, diventa un diplomatico che lo zar invia a Odessa, sul Mar Nero. 

Tra poco diremo perché e in che situazione. Ora cerchiamo di richiamare alla memoria chi è Eulero. Anche perché Paolo Maria Mariano (giustamente, nell’economia del suo romanzo) non lo fa in maniera particolareggiata. Sarà un lungo inciso, perché Eulero è un grande matematico.

Leonhard Euler, Jakob Emanuel Handmann, 1756, olio su tela, Museo d'arte di Basilea

Leonhard Euler – italianizzato Eulero – nasce e studia a Basilea, in Svizzera. Il suo maestro è un altro grande matematico, Johann della saga dei Bernoulli. Nel 1726, a 19 anni, vince un premio dell’Académie des Sciences di Parigi per un lavoro sull’alberatura delle navi. L’innovazione tecnologica e le esigenze pratiche sono alla base dello sviluppo scientifico europeo proprio come lo sviluppo scientifico è alla base dell’innovazione. Le due dimensioni coevolvono e così molto spesso questo rapporto coevolutivo lo troviamo espresso nella medesima persona. Euler è una di queste che, a ben vedere, rappresentano il carattere distintivo della società europea.

Ed è proprio in una dimensione europea – tra Svizzera, Francia, Germania e Russia – che si esprime l’eclettica propensione di Eulero. Dopo Parigi e Basilea, infatti, lo troviamo a San Pietroburgo, dove giunge al seguito di un altro dei fratelli Bernoulli, Daniel; poi a Berlino e poi ancora in Russia, con Caterina la Grande.

Certo, tra i suoi molteplici interessi, il principale è la matematica. E infatti Eulero contribuisce a sviluppare non solo il calcolo infinitesimale e le equazioni differenziali, ma anche la geometria, la teoria dei numeri, lo studio delle serie e il calcolo delle variazioni. Si concentra sul concetto di funzione e propone di considerarne il valore primario in matematica, non prima di contribuire a chiarirne il significato. È lui, infatti, che ne dà finalmente una definizione precisa: per Euler la funzione è una qualsiasi espressione analitica formata in qualsiasi modo da una quantità variabile e da costanti. Inoltre distingue tra funzioni algebriche, quelle che richiedono di applicare solo operazioni algebriche sulla variabile indipendente; a loro volta distinte in razionali (richiedono l’uso solo delle quattro operazioni) e irrazionali (richiedono anche l’uso dei radicali); funzioni trascendenti, che richiedono operazioni trigonometriche, logaritmiche, esponenziali; funzioni a più variabili.   

Com’è nello spirito del tempo, Eulero cerca costantemente di applicare le sue ricerche matematiche alla fisica, creando sia la meccanica analitica (alternativa alla vecchia meccanica geometrica) sia la meccanica dei corpi rigidi. I suoi apporti allo studio delle maree e i suoi libri sulla scienza della navigazione – Scientia navalis (1749) e Théorie complète de la construction et de la manouvre des vaisseaux (1773) – non si fermano sulla soglia delle accademie, ma risultano fondamentali per la marineria europea. Potremmo dire, fondamentali per la superiorità della marineria europea. 

Eulero si interessa anche di geografia e di cartografia. Sua è una dettagliata mappa della Russia, disegnata di propria mano. Né sono da meno i suoi studi nel campo dell’ottica, dell’acustica, della scienza dei materiali. E dell’idrodinamica: è lui che elabora le equazioni fondamentali per lo studio del moto di un fluido ideale. Si interessa inoltre di calore – di quel calore che è il tema emergente nella nascente industria europea meccanizzata – giungendo molto vicino alla sua spiegazione causale. Nella sua Dissertatio de igne (1739) ipotizza infatti che il calore sia dovuto all’oscillazione di corpuscoli.

Malgrado non si occupi solo di matematica, ma anche e piuttosto intensamente di fisica e di sviluppo tecnologico, è, con ogni probabilità, il più prolifico matematico di tutti i tempi: scrive in media ottocento pagine l’anno; le sue memorie si contano a centinaia, l’insieme delle sue opere riempie 74 interi volumi. La produttività di Eulero non viene meno neppure negli ultimi diciassette anni della sua vita, quando resta completamente cieco. Malgrado non abbia più occhi per vedere, pubblica molti libri e quattrocento lavori. Non c’è solo quantità, in quelle pagine. Ammirato ovunque, scrive lo storico della matematica Morris Kline: «alla fine della sua vita egli [potrà] considerare suoi allievi tutti i matematici europei» e non solo la voce narrante del romanzo di Mariano. 

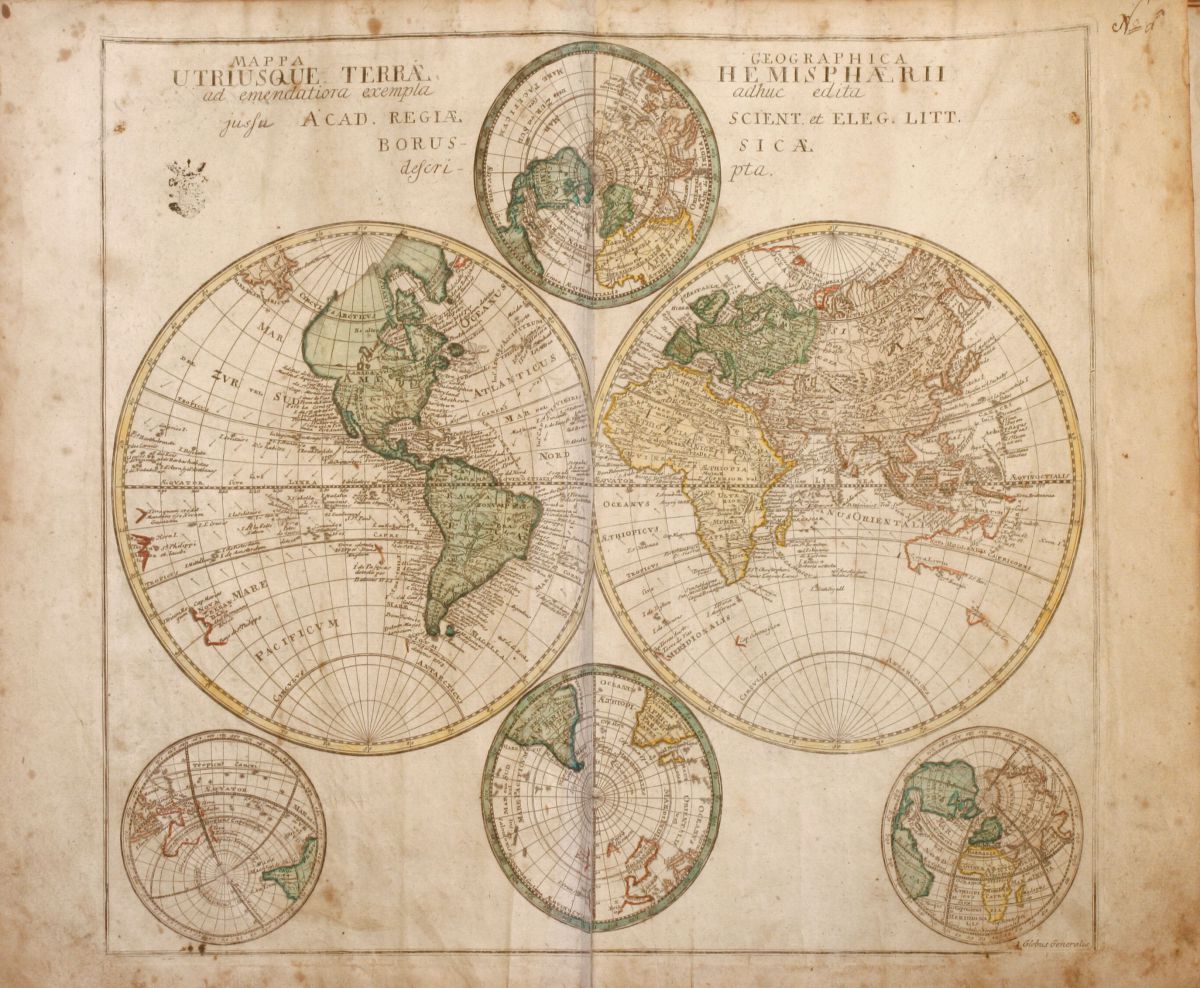
Leonhard Euler, Geographischer Atlas bestehend in 44 Land-Charten, 1760, Berlino

Ebbene, questo personaggio, Eulero, contribuisce come nessun altro allo sviluppo del calcolo infinitesimale e alla sua rapida affermazione, anche al di fuori dalla stretta dimensione matematica. La sua Introductio in analysin infinitorum del 1748 è considerata la prima presentazione completa del calcolo infinitesimale, inventato (o scoperto) da Isaac Newton e in maniera indipendente da Gottfried Leibniz qualche decennio prima. Le Institutiones calculi differentialis del 1755 e le Institutiones calculi integralis in tre volumi, scritti tra il 1768 e il 1780, costituiscono poi due punti di riferimento imprescindibili per gli sviluppi del calcolo infinitesimale.     

Se una delle conseguenze dello sviluppo del calcolo infinitesimale a opera di Eulero è la precisazione del concetto di funzione, la principale consiste nella precisazione del concetto di integrale. Per tutto il Settecento l’integrale è considerato o come inverso della derivata o come inverso del differenziale. E se Newton lo considera un’antiderivata, Leibniz lo definisce come la somma dei differenziali. Johann Bernoulli, seguendo Leibniz, lo considera come l’inverso del differenziale. Per Eulero, invece, il calcolo integrale non è la somma di differenziali ma la ricerca di una funzione. E se anche introduce il concetto di “sommazione”, lo fa solo per poter ottenere il valore approssimato di un integrale. 

Abbiamo già scritto molto, ma certo non è ancora abbastanza per caratterizzare la figura Eulero. Non fosse alto perché, come scrive Carl Boyer: «nessun altro singolo matematico, da solo, [ha contribuito] in così larga misura come lui, con la sua felice invenzioni di notazioni, a dare alla matematica la forma che essa presenta ancora oggi».  Per avere un’idea dell’importanza che assume Euler nella storia della matematica, basti ricordare che è sua la formula considerata la più bella e (quindi) la più significativa della scienza dei numeri:

L’equazione contiene i tre simboli (e, π e i) e i due numeri (1, 0) principali della matematica e li mette in relazione nel modo più semplice e (quindi) elegante. In poche parole, Eulero è il più grande matematico del XVIII secolo e uno dei più grandi di ogni tempo. Ai fini della nostra storia diciamo che è molto vicino a Caterina II di Russia, imperatrice non a caso “la Grande”.

Ci siamo soffermati un po’ di più su Eulero perché la figura del matematico aleggia costantemente nel romanzo di Mariano, anche se non è presente. Gli occhi di Eulero non è un romanzo su Eulero. Ma su qualcuno che vede la storia srotolarsi sotto occhi – quelli dell’ex garzone divenuto alto diplomatico – che osservano come se fossero di Eulero. Con matematica lucidità. Ma anche con un sentimento trattenuto, ma forte. 

Dice di sé la voce narrante:

Avrei trasportato forse carbone se il caso, un altro nome del destino, non mi avesse portato nella casa di Eulero, se non ci fosse stata Olga, se poi Nikolas Fuss non mi avesse insegnato le lingue e altro, se ancora Eulero non mi avesse fatto entrare nel ginnasio dell’Accademia, se poi non avesse parlato di me a chi era vicino alla famiglia reale, e se loro non avessero considerato utile affidarmi quegli incarichi che mi hanno portato dove sono.

Per la cronaca, Olga è quella che ha insegnato a leggere e a scrivere al giovanissimo garzone e Nikolas Fuss è il segretario di Eulero: un personaggio storico, anch’egli svizzero di nascita e matematico valente.

E dov’è l’adesso della voce narrante. In successione Odessa, poi Venezia, infine di nuovo in Russia. È in questi viaggi che “gli occhi di Eulero” incontrano la storia e la descrivono con lucidità solo in apparenza distaccata. Non è la storia del matematico, ma la storia politica e culturale. E sanitaria. Perché a Odessa l’ex garzone di Eulero e ora alto diplomatico di Russia incontra Richielau. Certo, non il famoso cardinale che ha governato in Francia nel Seicento, ma il generale Armand Emmanuel de Vignerot du Plessis, duca di Richelieu, che su nomina dello zar è il governatore della città ucraina. E lo incontra, la voce narrante, mentre Napoleone è intento alla campagna di Russia (1812).

Lo grande storia, dunque, aleggia proprio come Eulero sul nostro romanzo. Ma l’alto diplomatico allievo di Eulero incontra a Odessa anche un’epidemia: una epidemia di peste. E racconta come i cittadini della città portuale, nel terrore, cerchino di fronteggiarla. Ecco, dunque, che nel romanzo entra da protagonista anche la storia della medicina. 

Nella Odessa martoriata non cessano le meschinità umane e, dunque, il romanzo ci offre anche uno spaccato del lato peggiore degli uomini. 

Infine Gli occhi di Eulero, dopo svariati cenni ad altri grandi del periodo, compreso Immanuel Kant, terminano di osservare ai funerali di Aleksandr Sergeevič Puškin, l’irrequieto poeta considerato il padre della moderna letteratura russa, morto in duello a San Pietroburgo il 29 gennaio 1837. La voce narrante lo accompagna alla sua ultima dimora ma non è tenero con lui, dal punto di vista della critica letteraria. A dimostrazione che sono occhi, quelli proposti da Paolo Maria Mariano, mai banali e mai conformisti. Come tutti gli occhi vedono un aspetto della realtà – vedono il mondo a modo loro – ma non si ritraggono dal prendere posizione. E sì che la posizione assunta da Paolo Maria Mariano è assolutamente ardita: entrare negli intrecci più complessi della storia. Dimostrare che ogni attività umana – dalla matematica alla letteratura – si svolgono in un mondo che ha carne e sangue. 

A nostro avviso il tentativo è riuscito.